Approximate relations between fine structure constant and first Feigenbaum constant

The - somehow mysterious - fine structure constant α (see for example Wikipedia), usually referred by its reciprocal 1/α ~ 137.035 999 074(44) (NIST value, 2012) is thought to be related with I(0,x), the modified Bessel function of the first kind of order 0, as you may easily see by a quick overlook on the net; see for example formula (1) at https://accelconf.web.cern.ch/accelconf/LINAC08/papers/tup080.pdf
I have found (using the Inverse Calculator on the web) an approximate formula linking them even with the - somehow mysterious - (first) Feigenbaum's constant δ=4.6692016091... (see for example Wolfram MathWorld or Wikipedia) by this relation

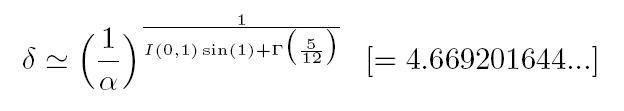
which is exact up a relative error less than 10^-8 (or, 1 over 100 millions); and it's inverse, more interesting,

which is exact up a relative error less than 3 10^-8.
That seems good enough, for a physical "constant" suspected of slight variations in time.
Bessel functions are notoriously related with goniometric functions and function Γ.
(Pay attention that here above α denotes - as used - the fine structure constant, not the second Feigenbaum constant 2.502907875... usually denoted by the same Greek letter.)

Alessandro Soranzo (2010-2012)