4.3 La distribuzione normale

 

Oltre alle variabili aleatorie discrete che abbiamo finora considerato, vi sono anche variabili aleatorie che possono assumere un insieme continuo di valori: la statura, oppure il peso, oppure la temperatura corporea sono delle grandezze che si potrebbero misurare, almeno in teoria, con una precisione molto accurata, ossia con molte cifre decimali. Tra le variabili aleatorie continue, la più rilevante è la variabile aleatoria con distribuzione normale, e come al solito, ne introduciamo lo studio per mezzo della seguente questione:

Problema introduttivo. Un oculista, sapendo che il glaucoma si manifesta sintomaticamente con un’alta pressione intraoculare, viene a sapere che in una certa popolazione la distribuzione dei valori di tale pressione è approssimativamente una “normale” con valore medio m = 16 mm Hg e deviazione standard s = 3 mm Hg. L’oculista sa anche che una persona che non manifesta tale malattia ha solitamente un valore compreso tra 12 e 20 mm Hg. Come può determinare la percentuale di popolazione con pressione maggiore del valore critico di 20 mm Hg?

 

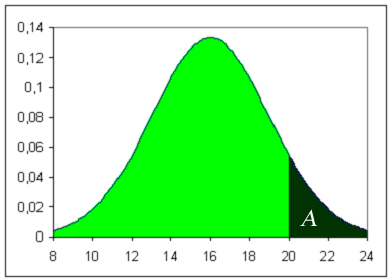
Affermare che la distribuzione dei valori di tale pressione è approssimativamente una normale con valore medio 16 mm Hg e deviazione standard 3 mm Hg significa che ci troviamo in una situazione che può essere descritta da un grafico di questo tipo:

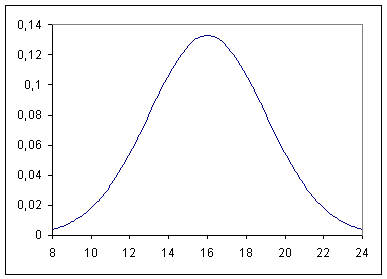
Osservando il grafico, possiamo dedurre immediatamente due fatti:

·        i valori pressori più frequenti sono quelli attorno al valor medio m = 16;

·        si nota una simmetria rispetto al valore medio, nel quale il grafico raggiunge il suo massimo.

Dobbiamo al matematico tedesco Karl Frederich Gauss la descrizione e lo studio dell’equazione di questa particolare funzione esponenziale dal grafico “a campana”, la quale per l’appunto viene detta gaussiana: dove, nel nostro caso, ,  e dove e indica il numero di

Nepero, approssimativamente uguale a  

Le variabili aleatorie caratterizzate da una funzione esponenziale di questo tipo vengono brevemente indicate con , e la lettera N indica che siamo in presenza di una distribuzione di probabilità normale con parametri m e s. Perciò, nel caso del nostro oculista, abbiamo stabilito che la distribuzione della pressione intraoculare è una variabile aleatoria , descritta dalla funzione .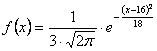

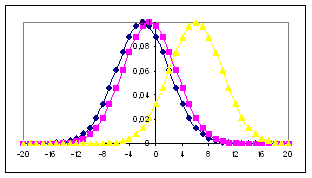
Siccome il grafico della gaussiana dipende dai valori m e s, la forma della “campana” cambierà al

variare di questi. In generale, possiamo osservare che: ·        al variare del valore medio m, il grafico della funzione viene traslato, verso sinistra se  m diminuisce, verso destra se  m cresce; ·        al variare della deviazione standard s, la campana si “stringe” e si “alza” se s diminuisce (ossia, se i dati si concentrano attorno alla media), oppure si “allarga” e si “schiaccia” se s aumenta (ossia, se i dati sono molto dispersi).

 

 

Ritorniamo ora al grafico iniziale: abbiamo dipinto di colore scuro la parte di piano (il cosiddetto sottografico della funzione) relativa alla popolazione con pressione superiore a 20 mm Hg, e di colore chiaro quella inferiore; la somma delle due aree ci dà evidentemente il 100% della popolazione. Da un punto di vista matematico, ciò

equivale a dire che l’area del sottografico delle gaussiane è sempre pari ad uno.

Pertanto, per risolvere il problema introduttivo, dobbiamo riuscire a calcolare l’area A della regione di colore scuro (che si chiama anche coda della gaussiana) in rapporto all’area totale della gaussiana. Coloro che conoscono il significato matematico dell’integrale sanno che è possibile arrivare al risultato determinando il valore:

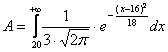
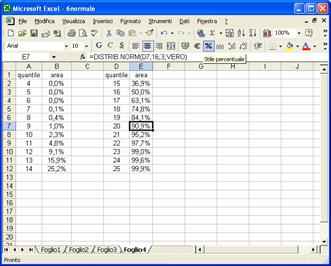
Noi, più semplicemente, desideriamo segnalare che con MS Excel è immediato calcolare la percentuale desiderata utilizzando la funzione:

DISTRIB.NORM(x; Media; Dev_standard; Cumulativo)

dove x è il quantile[1] su cui si calcola la distribuzione, Media, ossia m, è il valore medio, Dev_standard, ossia s, è la deviazione standard della distribuzione ed infine Cumulativo è un valore logico (o VERO o FALSO), che ci consente di chiedere nel primo caso la percentuale di area fino al quantile x (l’area colore chiaro), oppure nel secondo caso di conoscere il valore della funzione gaussiana nel quantile x. Nel nostro caso,

DISTRIB.NORM(20; 16; 3; VERO) fornisce la percentuale di persone con pressione fino a 20 mm Hg, precisamente il 90,9%. Concludendo, il valore cercato della percentuale di popolazione con pressione introculare maggiore di 20 si ottiene prendendo il complementare:

Le cose appaiono forse ancor più chiare se si fa ricorso al linguaggio della probabilità: tenendo conto del fatto che il sottografico della gaussiana ha esattamente area uguale ad 1, ed 1 è anche il valore della probabilità che si manifesti l’evento certo, per la nostra variabile aleatoria X riesce che:

e dunque, l’area vale:

 

La distribuzione normale riveste grande importanza in statistica poiché molti fenomeni naturali possono essere descritti per suo tramite. In particolare, la sua simmetria è una caratteristica essenziale: imbattersi in soggetti caratterizzati da valori molto superiori alla media è un evento tanto improbabile quanto quello di imbattersi in valori di molto inferiori.

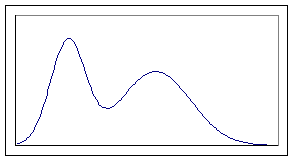
Tuttavia, vi sono casi in cui questo modello non è applicabile, come si vede nella distribuzione bimodale[2] riportata qui a fianco, nella quale prevalgono due valori caratterizzati da maggiore frequenza, oppure come osservato nello Spunto di Riflessione della Appendice 1. Altre variabili aleato

rie continue molto utilizzate sono le distribuzioni t di Student o le distribuzioni , di cui ci proponiamo di parlare in una prossima dispensa.

 

 

Succede in molte situazioni pratiche di dover utilizzare la variabile aleatoria , la normale standardizzata, ossia la variabile aleatoria normale di valor medio  e di deviazione standard . Ogni libro di statistica ne riporta apposite tavole ed indica anche il modo per trasformare una distribuzione normale  in una standardizzata  (si veda ad esempio [6]). Per tale distribuzione MS Excel dispone della funzione DISTRIB.NORM.ST(z) essendo z (e non più, stranamente, x) il quantile. MS Excel

dispone anche delle due “funzioni inverse”, INV.NORM e INV.NORM.ST, che permettono di determinare i quantili partendo dai valori della distribuzione. Ad esempio, abbiamo visto che l’istruzione DISTRIB.NORM(20; 16; 3; VERO) restituisce il valore numerico 0,909 (ossia il 90,9% di probabilità). Al contrario, l’istruzione INV.NORM(0,909; 16; 3) restituisce come risultato 20.

Per mezzo di queste ultime funzioni, possiamo risolvere i seguenti problemi: