4.2 La distribuzione binomiale
|
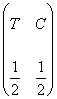
L’esempio classico, ma allo stesso tempo utile, con cui partire è il lancio di una monetina, nel classico gioco di testa T o croce C. Qui a fianco, vedete visualizzata la variabile aleatoria, con la relativa probabilità degli esiti. La domanda che ci poniamo è: Se lanciamo per tre volte la monetina, qual è la probabilità P di ottenere complessivamente due volte testa? |
|
|
|
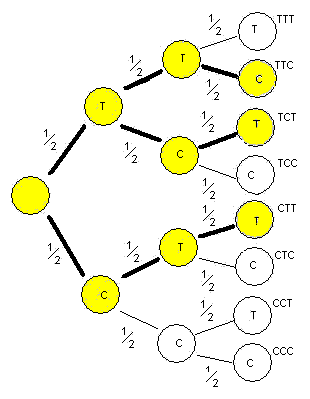
In altri termini, qual è la probabilità P di ottenere una sequenza in cui vi siano due teste e una croce, indifferentemente dall’ordine
con cui questo accade? Si tratta di un problema che si risolve facilmente se lo si visualizza con un grafo ad albero. Partendo dal nodo
centrale, possiamo camminare verso l’alto o verso il basso con probabilità |
|
|
. 
. Ci sono 
Tale probabilità 
equivale precisamente al
rapporto tra i soli 3 casi a noi favorevoli rispetto agli 8 casi possibili (e,
come si dice, equiprobabili tra loro).
|
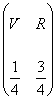
Ora passiamo ad esaminare un esperimento abbastanza simile: abbiamo un sacchetto con quattro palline di ping pong, una di colore verde (V) e tre rosse (R). La variabile aleatoria è quindi quella qui a fianco. Se facciamo caso, è come avere una moneta “truccata”, che dà una faccia con probabilità un quarto, e l’altra con probabilità tre quarti. |
|
La domanda ora è: se
effettuiamo 11
estrazioni totali, ogni volta reimbussolando, qual è la probabilità P di
ottenere in tutto esattamente 5 volte
la pallina V e 6 volte la pallina R, in un qualsiasi ordine?
Siccome in questo caso realizzare un grafo è un affare a
dir poco tedioso, proviamo a ragionare sulle sequenze di esiti.
Se volessimo avere esattamente la pallina verde alla
prima estrazione, ossia l’evento V,
la probabilità sarebbe 
. Se volessimo esattamente la
sequenza VV, la probabilità sarebbe 
. Se invece volessimo ottenere
precisamente la sequenza (di sette estrazioni) VVVVVRR, avremmo dunque 
. Dunque, la sequenza “di base” di undici
estrazioni VVVVVRRRRRR ha probabilità
. Abbiamo stabilito che a noi vanno bene tutte le sequenze
che sono degli anagrammi della precedente, come VRVRRVVRRVR oppure RVRVRRRVRVV.
Il numero di complessivo di tutti i possibili anagrammi è
abbastanza elevato, ce ne sono infatti:
(e se questi simboli appaiono
sconosciuti, in Appendice 4 si può trovare un richiamo sul calcolo
combinatorio). Se perciò vi sono 
casi favorevoli,
ciascuno avente la medesima probabilità della sequenza “di base”,
otteniamo la risposta al quesito:
P(5 Verdi
in 11 estrazioni) =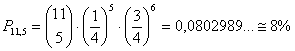 
Più in generale, quello che accade in un processo bernoulliano 
, ossia in una sequenza di n prove indipendenti, ciascuna avente due soli casi possibili
(successo ed insuccesso) con probabilità di successo p costante nelle varie prove (e ovviamente 1-p quella di insuccesso) è che la
probabilità di avere in n prove un
totale di k successi vale:
Con Excel, abbiamo a disposizione la funzione DISTRIB.BINOM per calcolare senza sforzo 
.
|
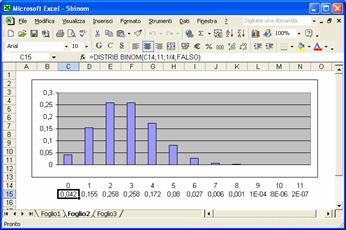
Pensiamo dunque di avere deciso di effettuare 11 estrazioni, e vogliamo quantificare le probabilità di avere zero estrazioni verdi, una estrazione verde, due, tre, .. , undici estrazioni verdi. Scriviamo perciò in riga i possibili valori di k, da zero ad undici. Per ottenere le probabilità che vedete qui a fianco, nelle celle inferiori, |
|
|
introduciamo la funzione di MS Excel DISTRIB.BINOM , che necessita di quattro informazioni: Num_successi, ossia k (cioè l’indirizzo della cella superiore), Prove, ossia n (cioè 11), Probabilità_s, ossia p, ed un valore logico[1] (VERO o FALSO), denominato Cumulativo, che ci potrebbe consentire di dare direttamente “la somma” delle probabilità; questo a noi ora non |
|
interessa affatto, per cui
scegliamo FALSO. I valori che otteniamo,
sono appunto le probabilità 
, 
, 
, …, 
. Come vedete, riuscire ad estrarre 9 volte
la pallina verde in 11 estrazioni è un evento di probabilità bassissima,
dell’ordine di 
. Computando le dodici probabilità, possiamo dar forma alla variabile aleatoria binomiale:
X =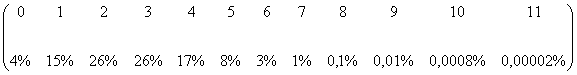 
Esercizio 7.
Fare 10 lanci di una moneta significa occuparsi di un processo bernouliano B(10, ½). Scopritene la variabile aleatoria per mezzo della funzione DISTRIB.BINOM come avete appena visto fare qui sopra.
Esercizio
8 (impegnativo).
Il problema dell’overbooking. Una casa
di cura privata convenzionata con il S.S.N. possiede 20 letti disponibili per interventi
di day hospital. Tuttavia, di solito accade che il 10% dei pazienti già
prenotati non si presenta all’appuntamento. Per tale motivo il CUP propone di accettare
fino ad un massimo di 22 prenotazioni al giorno. E’
una buona scelta oppure è rischiosa? In altri termini, qual è la probabilità di
ritrovarsi con almeno un paziente (inferocito) che non trova un letto pronto ad
accoglierlo? (suggerimento: si tratta di un B(22,
)…)
Esercizio 9.
Come si potrebbero simulare mille lanci di tre monetine e verificare che l’evento “escono due teste” ha probabilità 3/8 ?
Si dimostra che per le variabili aleatorie binomiali, cioè quelle caratterizzate da un processo bernoulliano , vale che 
e che 
.
Ricordiamo che esistono anche altre distribuzioni di probabilità disponibili tra le funzioni di Excel, inerenti a variabili aleatorie discrete. Ad esempio, la funzione POISSON relativa all’omonima distribuzione, che riguarda eventi caratterizzati da un numero di prove (osservazioni) n “molto grandi” con probabilità p di successo “molto piccole”, come accade ad esempio nella diffusione di malattie rare in una popolazione. La distribuzione è utile perché permette di evitare difficoltà di computazione legate al calcolo del fattoriale.