4.1 Le variabili aleatorie

            Questo paragrafo costituisce una sorta di intermezzo, per introdurre il concetto di variabile aleatoria, uno strumento matematico essenziale per la comprensione degli argomenti statistici che seguiranno. Aleatorio (dal latino alea, dado) significa casuale; come lo sono, del resto, i numeri che escono di volta in volta dal lancio di un dado. Iniziamo proprio da questo punto.

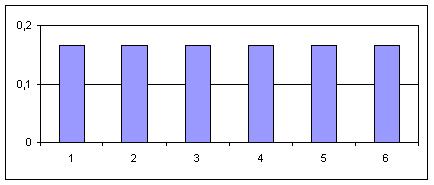
Questo “schemino” è una traduzione in linguaggio matematico del lancio di un dado non truccato: sulla prima riga appaiono i possibili esiti, i numeri da 1 a 6, ed in loro corrispondenza nella riga inferiore è riportata la probabilità (un sesto) che ciascuno di questi esiti si manifesti in un
lancio. Le medesime informazioni che abbiamo riassunto in quella tabella, si possono visualizzare con un istogramma. Le sei colonne di uguale altezza ci dicono che tutti i sei eventi hanno

la medesima probabilità  di uscita.

Cosa accade se invece giochiamo con due dadi? Ognuno concorda sul fatto che il 2, come somma, deve uscire in maniera molto meno frequente del 7. Infatti, basta dare un’ occhiata alla copertina del libro [4] di matematica di quando si andava al Liceo: il 2 si ottiene solo se il dado rosso (quello inferiore) e il dado verde (quello superiore) danno contemporaneamente uno. Il 7 invece si può ottenere in ben sei modi diversi, quelli individuabili sulla diagonale dell’immagine: .

            In pratica, raggruppando i 36 eventi possibili e contandoli “in diagonale”, possiamo creare  un altro schemino:

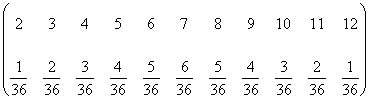
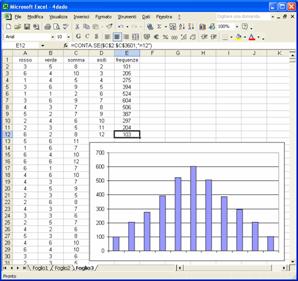
Osserviamo cosa accade se simuliamo con Excel una serie di 3600 lanci dei due dadi nelle colonne A e B, nella colonna C ne calcoliamo la somma, e nella colonna E contiamo quante volte sono usciti il 2, il 3, ... per mezzo delle istruzioni: =CONTA.SE($C$2:$C$3601;"=2") =CONTA.SE($C$2:$C$3601;"=3") e così via… Il grafico che si ottiene dal conteggio delle frequenze assolute manifesta un comportamento del tutto analogo a quello relativo alle
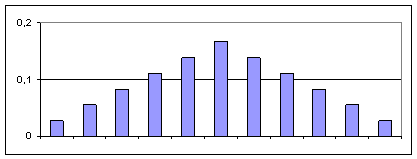
probabilità teoriche che avevamo conteggiato “in diagonale” e ci avevano permesso di realizzare lo schemino precedente, che possiamo a questo punto rappresentare con l’istogramma

delle frequenze relative, che vediamo qui sopra. Se ne avete voglia, vi consigliamo di dare un’occhiata al sito [7] alla voce “Esperimento dei dadi”, con il quale potete vedere come vanno le cose con un numero elevato di dadi (fino a venti). Oppure, provate voi a fare questo esercizio con Excel:

 

Quegli schemini che abbiamo appena visto sono due esempi di variabili aleatorie discrete. Si chiamano “variabili” perché l’esito “varia” di volta in volta, “aleatorie” perché imprevedibili, e “discrete” (in contrapposizione al termine “continue”) perché possono avere solo una quantità numerabile di esiti. Sui libri di testo specialistici vengono riportate definizioni ben più precise; si veda ad esempio Rosner [6].

            Ogni variabile aleatoria 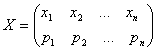 si può caratterizzare con due valori numerici, che forniscono un indice di posizione ed un indice di dispersione, al pari di quanto avevamo visto in Appendice 1 per media e varianza di una serie di dati: il valore atteso (detto anche valor medio o speranza matematica), , e la varianza, . Il valore atteso è definito in questo modo:

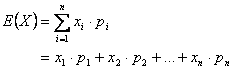
Quindi nel caso del lancio di un dado , mentre nel lancio di due dadi risulta .

Per quanto riguarda la varianza, essa è definita in questo modo:

e perciò nel lancio di un dado, risulta:

mentre nel lancio di due dadi risulta .

Qui siamo interessati ad un paio di variabili aleatorie molto importanti, la distribuzione binomiale e la distribuzione gaussiana. Vediamole assieme.