i dataset del corso
studentiannoscorso.txt
vaevt.txt
swelling.txt
tubi.txt
Facoltà di Medicina e Chirurgia a.a. 2009-2010
Corso di Laurea Magistrale in Biotecnologie Mediche
Corso Integrato di Innovazione Biotecnologica
Analisi Multivariata dei Dati Sperimentali
L'analisi di sopravvivenza
scegliere un modello per spiegare i dati "time to event"
- alcune slides introduttive
esito1 <- numeric(1000)
esito2 <- numeric(1000)
esito3 <- numeric(1000)
for ( j in 1:1000) {
dado <- sample(1:6, 100, replace = T)
esito1[j] <- min(which(dado == "1"))
esito2[j] <- min(which(dado < "3"))
esito3[j] <- min(which(dado < "4"))
}
boxplot(esito1, esito2, esito3)
# rm (list = ls() )
www <- "http://www.dmi.units.it/~borelli/biotec/tubi.txt"
tubi <- read.table( www , header = TRUE )
attach(tubi)
tubi[1:10,]
Vediamo (in maniera rozza) al variare del type varia il tempo di percolazione
boxplot(time ~ type)
Non dobbiamo però trascurare i dati censurati:
time
status
table(status, time)
library(survival)
Surv(time, status)
calcoliamo lo stimatore di Kaplan e Meier
kaplan_meier <- survfit(Surv(time, status) ~ type)
kaplan_meier
summary(kaplan_meier)
rappresentiamo le curve di sopravvivenza e raffrontiamole con i boxplot
par(mfrow = c(1,2))
plot(kaplan_meier, lty=c(5,3), xlab="Leakage time (hours)")
boxplot(time ~ type)
par(mfrow = c(1,1))
Test statistico "Log-rank": non vi è differenza tra le due curve di sopravvivenza?
logrank <- survdiff( Surv(time, status) ~ type)
logrank
Spesso si ipotizza che il rischio tra due curve sia proporzionale. In tal caso, si suppone che la funzione di rischio baseline sia del tipo h0(t) = \lambda \rho t ^ ( \rho - 1) , essendo \lambda il parametro di scala e \rho il parametro di forma.
? pweibull
Abbiamo quindi a disposizione la descrizione loglineare del modello di sopravvivenza:
log ( Ti
) = \mu + xi \alpha + \sigma Ei
dove \mu è l'intercetta e \sigma rappresenta la scala:
modellologlineare <- survreg( Surv(time, status) ~ type, dist="weibull")
summary(modellologlineare)
- per interpretare l'output di survreg abbiamo a disposizione il capitolo 1 di Duchateau e Janssen
Deduciamo dunque che \lambda = exp( - \mu / \sigma) e che \rho = 1 / \sigma:
summary(modellologlineare)
mu <- as.table(summary(modellologlineare)[[7]])[[1]]
mu
sigma <- summary(modellologlineare)[6][[1]]
sigma
lambda <- exp ( - mu / sigma )
lambda
rho <- 1 / sigma
rho
La diagnostica del modello richiede di verificare la proporzionalità del rischio:
plot(survfit(Surv(time, status) ~ type), lty=1:2, fun="cumhaz", main = "Diagnostica")
Scopriamo ("approssimativamente") se la PEEP ha avuto un ruolo:
summary(survreg( Surv(time, status) ~ type + peep , dist="weibull") )
Teniamo presente che però la covariata PEEP cambia nel tempo (stimatore di Breslow Aalen, library timereg)
Ultimo "compito per casa" da inviarmi per posta. Indicate nell'oggetto: Cognome 4 (es. Borelli 4) Utilizzate le funzioni survreg e coxph per analizzare se nel dataset bisturi.txt (cortesia prof. N. de Manzini e dott. M. Giuricin) il tipo di bisturi, gli anni della paziente ed il tipo di intervento influiscono sul tempo di degenza , eventualmente censurato dall'evento dimissione . Quali conclusioni potete trarre? |
- usualmente si usa la libreria survival, oppure timereg. La libreria coin dei test di permutazione è altrettanto utile
- il dataset glioma di Chiara Maria Grana
library("HSAUR")
library("survival")
library("coin")
data("glioma", package = "coin")
glioma[1:10,]
glioma[30:37,]
- scopriamo come è fatto un oggetto Surv
glioma$event
Surv(glioma$time, glioma$event)
- dividiamo in due parti il dataset, a seconda dell'istologia
g4 <- subset(glioma, histology = "GBM")
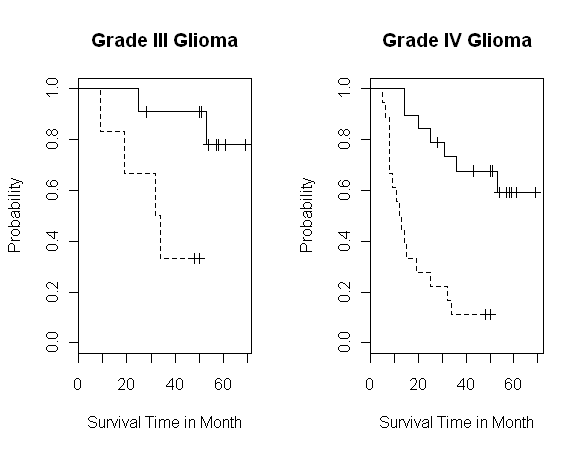
- ecco le curve di sopravvivenza (clic sull'immagine per il codice)
- Iniziamo con gli stimatori di Kaplan Meier. Possiamo effettuare il Logrank test esatto per mezzo della library coin
surv_test(Surv(time, event) ~ group, data = g4, distribution = "exact")
- oppure possiamo effettuare il Logrank test (secondo Harrington e Fleming) con la library survival
survdiff(Surv(time, event) ~ group, data = g3)
survdiff(Surv(time, event) ~ group, data = g4)
- invece di suddividere il dataset in due sottoinsiemi, sarebbe interessante scoprire se la nuova radioimmuno terapia "RIT" è superiore per entrambi i gruppi (grado III e grado IV); questo di può fare stratificando (o blocking) rispetto al grado del tumore, con un Logrank test approssimato
- Vediamo ora di introdurre covariate con il modello di Cox. Analizziamo il dataset GBSG2 di M. Schumacher
data(GBSG2, package ="ipred")
- Fittiamo un modello a rischio proporzionale di Cox
cox1
summary(cox1)
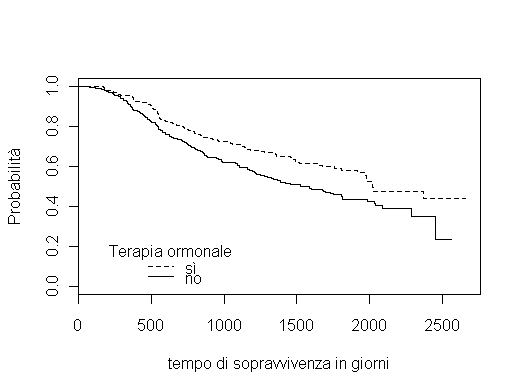
- possiamo fornire una stima del rischio relativo per le pazienti con terapia ormonale
exp(cbind(coef (cox1) , ci) ) ["horThyes" , ]
- dunque, le pazienti con terapia ormonale hanno un rischio relativo inferiore (fattore protettivo), e quindi una migliore sopravvivenza
- la
diagnostica
dei modelli di regressione non è semplice (non ci sono
"residui"). Per verificare l'ipotesi di proporzionalità del
rischio, si prova a vedere se le stime dei coefficienti non variano nel
tempo
regcoefftempo
- dunque, vi sono indicazioni che l'età e il grade del tumore cambino con il tempo. Lo vediamo anche con plot(regcoefftempo, var = "age" ) e plot(regcoefftempo, var = "tgrade.L" )
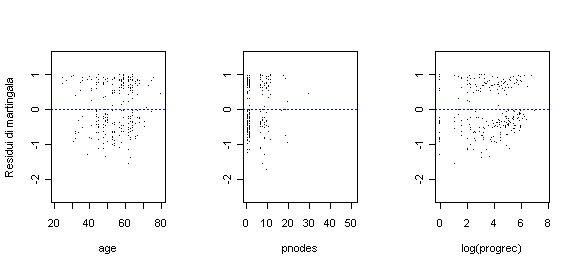
- un'altra diagnostica si può effettuare per mezzo delle martingale, osservando se il grafico dei residui di martingala hanno una deviazione sistematica dallo zero vs. le covariate; qui pare di no
- scaricando ed installando inoltre la library("party") si può combinare l'analisi di sopravvivenza alla ricerca di alberi condizionali che ripartiscono il dataset
library("party")
albero1 <- ctree (Surv(time, cens) ~ . , data = GBSG2)
plot (albero1)
- il numero di linfonodi positivi pnodes è la variabili più importante (si veda il p value della regressione di Cox). Le donne con meno di tre linfonodi che hanno avuto accesso alla terapia ormonale hanno apparentemente avuto una prognosi migliore di quelle con alto numero di linfonodi e un basso livello dei recettori al progesterone progrec
- esercizio. Oltre al modello non parametrico coxph abbiamo a disposizione survreg, un modello parametrico generico. Possiamo esercitarci seguendo l'articolo di Viv Bewick : ecco i codici per generare le figure 2 (regressione) e 3 (diagnostica)
www <- "http://www.dmi.units.it/~borelli/biotec/bewick.txt"
bewick <- read.table( www , header = TRUE )
attach(bewick)
plot(survfit(Surv(giorni, stato) ~ trattamento), main ="Figure 2", xlab="Survival time(days)", ylab="Probability of survival", lty= c(2,1))
plot(survfit(Surv(log(giorni), stato) ~ trattamento), lty=1:2, fun="cumhaz", main = "Figure 3 - Diagnostica")
summary(coxph(Surv(giorni, stato) ~ trattamento + eta))
summary(survreg(Surv(giorni, stato) ~ trattamento + eta))